LC 128场双周赛

100280. 覆盖所有点的最少矩形数目 - 力扣（LeetCode）

给你一个二维整数数组 point ，其中 points[i] = [xi, yi] 表示二维平面内的一个点。同时给你一个整数 w 。你需要用矩形 覆盖所有 点。

每个矩形的左下角在某个点 (x1, 0) 处，且右上角在某个点 (x2, y2) 处，其中 x1 <= x2 且 y2 >= 0 ，同时对于每个矩形都 必须 满足 x2 - x1 <= w 。

如果一个点在矩形内或者在边上，我们说这个点被矩形覆盖了。

请你在确保每个点都 至少 被一个矩形覆盖的前提下，最少 需要多少个矩形。

注意：一个点可以被多个矩形覆盖。

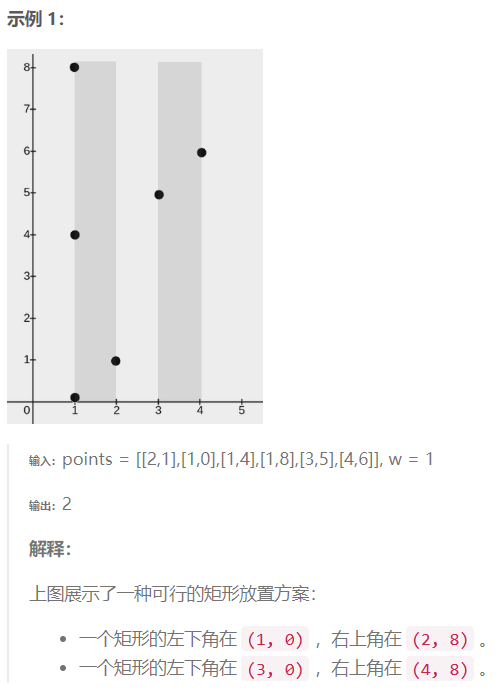
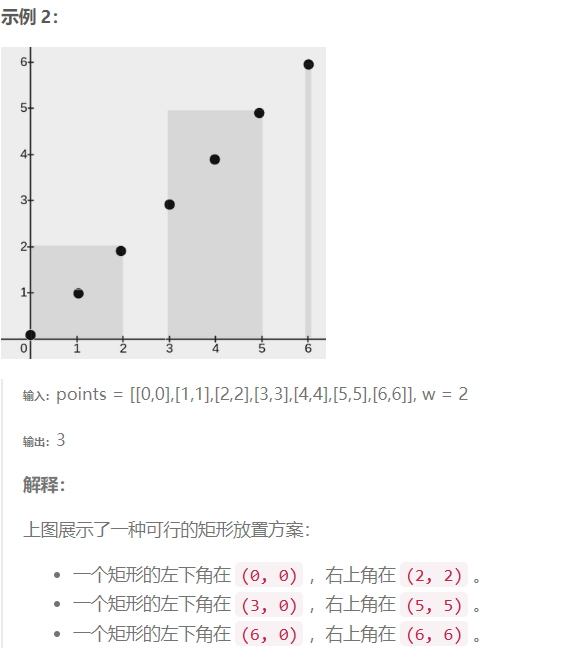
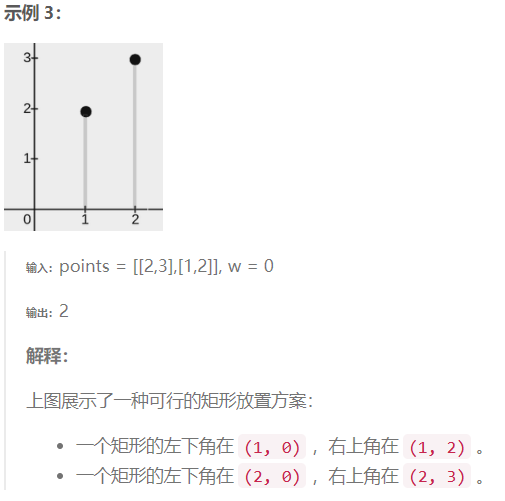
提示：

• 1 <= points.length <= 105
• points[i].length == 2
• 0 <= xi == points[i][0] <= 109
• 0 <= yi == points[i][1] <= 109
• 0 <= w <= 109
• 所有点坐标 (xi, yi) 互不相同。

可以这样进行理解最后答案的数目与高度是没有啥关系的（可以将它想象成一条线上的点），所以按照第一列的大小顺序进行排序，当每一次的宽度够不到下一个点的左区间的时候+w，同时ans + 1，如此反复贪心下去（但就是想不到）

如果这么写的话有一些像我之前写过的区间合并了

class Solution {
    public int minRectanglesToCoverPoints(int[][] points, int w) {
        //按照第一列的大小顺序进行排序
		Arrays.sort(points, (a, b) ->(a[0] - b[0]));
        int ans = 0, mx = -1, n = points.length;
        for(int i = 0; i < n; i++){
            if(points[i][0] > mx){
                ans += 1;
                mx = points[i][0] + w;
            }
        }
        return ans;
    }
}

100273. 边界元素是最大值的子数组数目 - 力扣（LeetCode）

给你一个 正 整数数组 nums 。请你求出 nums 中有多少个子数组，满足子数组中 第一个 和 最后一个 元素都是这个子数组中的 最大 值。

示例 1：

输入：nums = [1,4,3,3,2]

输出：6

解释：

总共有 6 个子数组满足第一个元素和最后一个元素都是子数组中的最大值：

• 子数组 [1,4,3,3,2]，最大元素为 1 ，第一个和最后一个元素都是 1 。
• 子数组 [1,4,3,3,2] ，最大元素为 4 ，第一个和最后一个元素都是 4 。
• 子数组 [1,4,3,3,2] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [1,4,3,3,2]，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [1,4,3,3,2] ，最大元素为 2 ，第一个和最后一个元素都是 2 。
• 子数组 [1,4,3,3,2] ，最大元素为 3 ，第一个和最后一个元素都是 3 。

所以我们返回 6 。

示例 2：

输入：nums = [3,3,3]

输出：6

解释：

总共有 6 个子数组满足第一个元素和最后一个元素都是子数组中的最大值：

• 子数组 [3,3,3]，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,3]，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。

所以我们返回 6 。

示例 3：

输入：nums = [1]

输出：1

解释：

nums 中只有一个子数组 [1] ，最大元素为 1 ，第一个和最后一个元素都是 1 。

所以我们返回 1 。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109

当遍历数组nums时，我们使用双端队列st来存储当前遍历到的元素的最大值及其出现次数。这样，在遍历过程中，我们可以快速地找到当前子数组的最大值，并更新答案ans。

class Solution {
    public long numberOfSubarrays(int[] nums) {
		long ans = nums.length;
		Deque<int[]> st = new ArrayDeque<>();
		st.push(new int[]{Integer.MAX_VALUE, 0});
		for(int x : nums){
			while(x > st.peek()[0]) st.pop();
			if(x == st.peek()[0]){
				ans += st.peek()[1]++;
			}else{
				st.push(new int[]{x, 1});
			}
		}
		return ans;
    }
}